【中国发明,中国发明授权】一种基于STL三维模型的曲面加工方法
有权-审定授权 中国
- 申请号:
- CN201410635076.1
- 专利权人:
- 常州工学院
- 授权公告日/公开日:
- 2017.05.03
- 专利有效期:
- 2014.11.12-2034.11.12
- 技术分类:
- G06:计算;推算;计数
- 转化方式:
- 转让
- 价值度指数:
-
- 62.0分
- 价格:
- 面议
- 专利信息&法律状态
- 专利自评
- 专利技术文档
- 价值度指数
- 发明人阵容
 著录项
著录项
- 申请号
- CN201410635076.1
- 申请日
- 20141112
- 公开/公告号
- CN104392030A
- 公开/公告日
- 20150304
- 申请/专利权人
- [常州工学院]
- 发明/设计人
- [丁仕燕, 干为民, 黄秀琴, 刘祖朋, 黄志荣, 何亚峰]
- 主分类号
- G06F17/50
- IPC分类号
- C12N 9/0008(2013.01) C12N 9/16
- CPC分类号
- C12N 9/0008(2013.01) C12N 9/16(2013.01)
- 分案申请地址
- 国省代码
- 江苏(32)
- 颁证日
- G06T1/00
- 代理人
- [高桂珍]
 摘要
摘要
本发明公开了一种基于STL三维模型的曲面加工方法,属于曲面加工技术领域。本发明的一种基于STL三维模型的曲面加工方法,将待加工曲面的STL三维模型进行投影,将组成待加工曲面的三角面片在三维空间内的计算转化为二维平面内的三角形计算,同时在构造矩形A1A2A3A4内实现球铣刀位置的搜索和计算,减少了数据采集量,大大简化了曲面加工刀位轨迹的计算,更加容易实现软件控制,且程序可读性好,运算量少,尤其适用于各点法矢量与Z轴夹角不大的STL曲面的加工。
 法律状态
法律状态
| 法律状态公告日 | 20220218 |
| 法律状态 | 专利申请权、专利权的转移 |
| 法律状态信息 | 专利权的转移 IPC(主分类):G06F 17/50 专利号:ZL2014106350761 登记生效日:20220208 变更事项:专利权人 变更前权利人:常州工学院 变更后权利人:常州苏双迈达精密机械有限公司 变更事项:地址 变更前权利人:213022 江苏省常州市新北区巫山路1号 变更后权利人:213000 江苏省常州市天宁区虹阳路2号 |
| 法律状态公告日 | 20170503 |
| 法律状态 | 授权 |
| 法律状态信息 | 授权 |
| 法律状态公告日 | 20150401 |
| 法律状态 | 实质审查的生效 |
| 法律状态信息 | 实质审查的生效 IPC(主分类):G06F 17/50 申请日:20141112 |
| 法律状态公告日 | 20150304 |
| 法律状态 | 公开 |
| 法律状态信息 | 公开 |
| 事务数据公告日 | 20220218 |
| 事务数据类型 | 专利申请权、专利权的转移 |
| 转让详情 | 专利权的转移 IPC(主分类):G06F 17/50 专利号:ZL2014106350761 登记生效日:20220208 变更事项:专利权人 变更前权利人:常州工学院 变更后权利人:常州苏双迈达精密机械有限公司 变更事项:地址 变更前权利人:213022 江苏省常州市新北区巫山路1号 变更后权利人:213000 江苏省常州市天宁区虹阳路2号 |
 权利要求
权利要求
权利要求数量(3)
独立权利要求数量(1)
1.一种基于STL三维模型的曲面加工方法,其包括以下步骤:
(1)已知待加工曲面的STL三维模型,将曲面的三维模型投影到二维坐标系O-XY中, 得到投影面S;组成待加工曲面的若干三角面片△ABC在二维坐标系O-XY中的投影为三角形 △A'B'C';
(2)创建并读取动点M(x M,y M);
(3)判断动点M(x M,y M)是否在投影面S中的某个投影三角形△A'B'C'上;根据判断 结果执行步骤(4)或(5);
(4)如果动点M在投影面S中的某个投影三角形△A'B'C'上,求出动点M(x M,y M)对 应的点P在三维坐标系O-XYZ中的坐标(x P,y P,z P),即球铣刀与对应三角面片△ABC的接 触点坐标,其中:x P=x M,y P=y M,
式中:z A、z B和z C分别表示三角面片△ABC中的A、B和C三点的在O-XYZ坐标系中的 z轴坐标,S △MB'C'、S △MA'C'、S △MA'B'和S △A'B'C'分别表示△MB'C'、△MA'C'、△MA'B'和△A'B'C'的面 积;则球铣刀与曲面的接触点P(x P,y P,z P)在O-XYZ坐标系中的位置矢量为:
P=(x P,y P,z P) T;
进而,求出球铣刀的球心O 1点在O-XYZ坐标系中的位置矢量O 1为:
式中:r为球铣刀的半径, 为球铣刀与曲面接触点 P所在三角面片△ABC的法矢量的单位矢量;重复步骤(2),读取下一个动点M(x M,y M), 并重复步骤(3),直至将所有动点M读取完毕;
(5)如果动点M不在投影面S中的某个投影三角形△A'B'C'上,则重复步骤(2),读取 下一个动点M(x M,y M),并重复步骤(3),直至将所有动点M读取完毕;
(6)顺序连接各点即可得到球铣刀加工STL曲面的刀位轨迹。
2.根据权利要求1所述的一种基于STL三维模型的曲面加工方法,其特征在于:步骤 (2)中的动点M的具体创建方法为:
(2-1)测出投影面S在二维坐标系O-XY的X轴方向上的最小值X min和最大值X max,以 及Y轴方向上的最小值Y min和最大值Y max;由X min、X max、Y min和Y max坐标值构造矩形A 1A 2A 3A 4; 设定球铣刀移动的步长和行距;
(2-2)将动点M(x M,y M)初始化,初始位置为矩形A 1A 2A 3A 4的左下角顶点A 1(X min, Y min),即x M=X min,y M=Y min;
(2-3)将动点M(x M,y M)沿平行X轴正方向逐一移动一个步长,直到x M>X max,完成 平行X轴的一行动点M的创建;
(2-4)将动点M(x M,y M)沿平行Y轴正方向移动一个行距,令x M=X max,并沿平行X 轴负方向逐一移动一个步长,直到x M (2-5)令x M=X min,重复步骤(2-3)、(2-4),直到y M>Y max,完成整个矩形A 1A 2A 3A 4 区域内的动点M的创建。
3.根据权利要求1所述的一种基于STL三维模型的曲面加工方法,其特征在于:步骤 (3)中判断动点M(x M,y M)是否在投影面S中的某个投影三角形△A'B'C'上的具体步骤为:
(3-1)读取一个三角面片△ABC,△ABC各点的坐标分别为A(x A,y A,z A),B(x B,y B, z B),C(x C,y C,z C);三角面片△ABC在二维坐标系O-XY中的投影三角形△A'B'C'各点的坐 标分别为A'(x A,y A),B'(x B,y B),C'(x C,y C);
(3-2)利用公式s △A'B'C'=s △MB'C'+s △MA'C'+s △MA'B'判断动点M是否在△A'B'C'上,式中, s △A'B'C'、s △MB'C'、s △MA'C、s △MA'B'分别表示△A'B'C'、△MB'C'、△MA'C'、△MA'B'的面积;根据 判断结果执行步骤(3-3)或(3-4);
(3-3)如果公式s △A'B'C'=s △MB'C'+s △MA'C'+s △MA'B'左右两边相等,则动点M在投影三角 形△A'B'C'上;
(3-4)如果公式s △A'B'C'=s △MB'C'+s △MA'C'+s △MA'B'左右两边不相等,则动点M不在投影 三角形△A'B'C'上;重复步骤(3-1)和(3-2),直至将组成待加工曲面的所有三角面片△ABC 数据读取完成。
1.一种基于STL三维模型的曲面加工方法,其包括以下步骤:
(1)已知待加工曲面的STL三维模型,将曲面的三维模型投影到二维坐标系O-XY中,得到投影面S;组成待加工曲面的若干三角面片△ABC在二维坐标系O-XY中的投影为三角形△A'B'C';
(2)创建并读取动点M(xM,yM);
(3)判断动点M(xM,yM)是否在投影面S中的某个投影三角形△A'B'C'上;根据判断结果执行步骤(4)或(5);
(4)如果动点M在投影面S中的某个投影三角形△A'B'C'上,求出动点M(xM,yM)对应的点P在三维坐标系O-XYZ中的坐标(xP,yP,zP),即球铣刀与对应三角面片△ABC的接触点坐标,其中:xP=xM,yP=yM,
z P = z A × S ΔM B ′ C ′ + z B × S ΔM A ′ C ′ + z C × S ΔM A ′ B ′ S Δ A ′ B ′ C ′ , ]]>
式中:zA、zB和zC分别表示三角面片△ABC中的A、B和C三点的在O-XYZ坐标系中的z轴坐标,S△MB'C'、S△MA'C'、S△MA'B'和S△A'B'C'分别表示△MB'C'、△MA'C'、△MA'B'和△A'B'C'的面积;则球铣刀与曲面的接触点P(xP,yP,zP)在O-XYZ坐标系中的位置矢量为:
P=(xP,yP,zP)T;
进而,求出球铣刀的球心O1点在O-XYZ坐标系中的位置矢量O1为:
O 1 = P + P O 1 = P + r ( x x 2 + y 2 + z 2 , y x 2 + y 2 + z 2 , z x 2 + y 2 + z 2 ) T , ]]>
式中:r为球铣刀的半径,为球铣刀与曲面接触点P所在三角面片△ABC的法矢量的单位矢量;重复步骤(2),读取下一个动点M(xM,yM),并重复步骤(3),直至将所有动点M读取完毕;
(5)如果动点M不在投影面S中的某个投影三角形△A'B'C'上,则重复步骤(2),读取下一个动点M(xM,yM),并重复步骤(3),直至将所有动点M读取完毕;
(6)顺序连接各点即可得到球铣刀加工STL曲面的刀位轨迹。
2.根据权利要求1所述的一种基于STL三维模型的曲面加工方法,其特征在于:步骤(2)中的动点M的具体创建方法为:
(2-1)测出投影面S在二维坐标系O-XY的X轴方向上的最小值Xmin和最大值Xmax,以及Y轴方向上的最小值Ymin和最大值Ymax;由Xmin、Xmax、Ymin和Ymax坐标值构造矩形A1A2A3A4;设定球铣刀移动的步长和行距;
(2-2)将动点M(xM,yM)初始化,初始位置为矩形A1A2A3A4的左下角顶点A1(Xmin,Ymin),即xM=Xmin,yM=Ymin;
(2-3)将动点M(xM,yM)沿平行X轴正方向逐一移动一个步长,直到xM>Xmax,完成平行X轴的一行动点M的创建;
(2-4)将动点M(xM,yM)沿平行Y轴正方向移动一个行距,令xM=Xmax,并沿平行X轴负方向逐一移动一个步长,直到xMmin;将动点M(xM,yM)沿平行Y轴正方向移动一个行距;
(2-5)令xM=Xmin,重复步骤(2-3)、(2-4),直到yM>Ymax,完成整个矩形A1A2A3A4区域内的动点M的创建。
3.根据权利要求1所述的一种基于STL三维模型的曲面加工方法,其特征在于:步骤(3)中判断动点M(xM,yM)是否在投影面S中的某个投影三角形△A'B'C'上的具体步骤为:
(3-1)读取一个三角面片△ABC,△ABC各点的坐标分别为A(xA,yA,zA),B(xB,yB,zB),C(xC,yC,zC);三角面片△ABC在二维坐标系O-XY中的投影三角形△A'B'C'各点的坐标分别为A'(xA,yA),B'(xB,yB),C'(xC,yC);
(3-2)利用公式s△A'B'C'=s△MB'C'+s△MA'C'+s△MA'B'判断动点M是否在△A'B'C'上,式中,s△A'B'C'、s△MB'C'、s△MA'C、s△MA'B'分别表示△A'B'C'、△MB'C'、△MA'C'、△MA'B'的面积;根据判断结果执行步骤(3-3)或(3-4);
(3-3)如果公式s△A'B'C'=s△MB'C'+s△MA'C'+s△MA'B'左右两边相等,则动点M在投影三角形△A'B'C'上;
(3-4)如果公式s△A'B'C'=s△MB'C'+s△MA'C'+s△MA'B'左右两边不相等,则动点M不在投影三角形△A'B'C'上;重复步骤(3-1)和(3-2),直至将组成待加工曲面的所有三角面片△ABC数据读取完成。
 说明书
说明书
技术领域
本发明涉及一种曲面加工方法,更具体地说,涉及一种基于STL三维模型的小曲率曲面加工方法。
背景技术
STL是最多快速原型系统所应用的标准文件类型,它使用三角形面片来表示三维实体模型,现已成为CAD/CAM系统接口文件格式的工业标准之一,绝大多数造型系统能支持并生成此种格式文件,现在越来越广泛地应用于数控加工中。STL文件由多个三角形面片数据组成,每个三角形面片包括三角形各个顶点的三维坐标及三角形面片的法矢量。三角形顶点的排列顺序遵循右手法则。
基于STL三维模型可以对各种曲面进行加工,然而,对于曲面进行加工时必须要有一个合适的运行轨迹,以保证曲面加工的顺利完成和加工曲面的精度。近年来,国内外学者针对曲面精加工轨迹的生成进行了大量的研究,提出了许多算法,主要可分为参数线法、截面法和投影法三类。现有的投影法通常是先在二维平面规划轨迹,并沿刀轴方向投影到被加工曲面或其等距面上形成刀轨,但是现有曲面刀位轨迹的计算方法普遍存在计算复杂繁琐、运行量大、且程序可读性差、软件实现困难的不足,限制了投影法在曲面加工中的应用。
发明内容
1.发明要解决的技术问题
本发明的目的在于克服现有曲面加工刀位轨迹计算方法复杂繁琐、运行量大、且程序可读性差、软件实现困难的不足,提供一种基于STL三维模型的曲面加工方法,采用本发明的技术方案,大大简化了曲面加工刀位轨迹的计算,采用更加直观简洁的计算方法,更加容易实现软件控制,且程序可读性好,运算量少,尤其适用于小曲率曲面的铣削加工。
2.技术方案
为达到上述目的,本发明提供的技术方案为:
本发明的一种基于STL三维模型的曲面加工方法,其包括以下步骤:
(1)已知待加工曲面的STL三维模型,将曲面的三维模型投影到二维坐标系O-XY中,得到投影面S;组成待加工曲面的若干三角面片ΔABC在二维坐标系O-XY中的投影为三角形ΔA′B′C′;
(2)创建并读取动点M(xM,yM);
(3)判断动点M(xM,yM)是否在投影面S中的某个投影三角形ΔA′B′C′上;根据判断结果执行步骤(4)或(5);
(4)如果动点M在投影面S中的某个投影三角形ΔA′B′C′上,求出动点M(xM,yM)对应的点P在三维坐标系O-XYZ中的坐标(xP,yP,zP),即球铣刀与对应三角面片ΔABC的接触点坐标,其中:xP=xM,yP=yM,
z p = z A × S Δ MB ′ C ′ + z B × S Δ MA ′ C ′ + z C × S Δ MA ′ B ′ S Δ A ′ B ′ C ′ , ]]>
式中:zA、zB和zC分别表示三角面片ΔABC中的A、B和C三点的在O-XYZ坐标系中的z轴坐标,SΔMB′C′、SΔMA′C′、SΔMA′B′和SΔA′B′C′分别表示ΔMB′C′、ΔMA′C′、ΔMA′B′和ΔA′B′C′的面积;则球铣刀与曲面的接触点P(xP,yP,zP)在O-XYZ坐标系中的位置矢量为:
P=(xp,yp,zp)T;
进而,求出球铣刀的球心O1点在O-XYZ坐标系中的位置矢量O1为:
O 1 = P + PO 1 = P + r ( x x 2 + y 2 + z 2 , y x 2 + y 2 + z 2 , z x 2 + y 2 + z 2 ) T , ]]>
式中:r为球铣刀的半径,球铣刀与曲面接触点P所在三角面片ΔABC的法矢量的单位矢量;重复步骤(2),读取下一个动点M(xM,yM),并重复步骤(3),直至将所有动点M读取完毕;
(5)如果动点M不在投影面S中的某个投影三角形ΔA′B′C′上,则重复步骤(2),读取下一个动点M(xM,yM),并重复步骤(3),直至将所有动点M读取完毕;
(6)顺序连接各点即可得到球铣刀加工STL曲面的刀位轨迹。
更进一步地,步骤(2)中的动点M的具体创建方法为:
(2-1)测出投影面S在二维坐标系O-XY的X轴方向上的最小值Xmin和最大值Xmax,以及Y轴方向上的最小值Ymin和最大值Ymax;由Xmin、Xmax、Ymin和Ymax坐标值构造矩形A1A2A3A4;设定球铣刀移动的步长和行距;
(2-2)将动点M(xM,yM)初始化,初始位置为矩形A1A2A3A4的左下角顶点A1(Xmin,Ymin),即xM=Xmin,yM=Ymin;
(2-3)将动点M(xM,yM)沿平行X轴正方向逐一移动一个步长,直到xM>Xmax,完成平行X轴的一行动点M的创建;
(2-4)将动点M(xM,yM)沿平行Y轴正方向移动一个行距,令xM=Xmax,并沿平行X轴负方向逐一移动一个步长,直到xMmin;将动点M(xM,yM)沿平行Y轴正方向移动一个行距;
(2-5)令xM=Xmin,重复步骤(2-3)、(2-4),直到yM>Ymax,完成整个矩形A1A2A3A4区域内的动点M的创建。
更进一步地,步骤(3)中判断动点M(xM,yM)是否在投影面S中的某个投影三角形ΔA′B′C′上的具体步骤为:
(3-1)读取一个三角面片ΔABC,ΔABC各点的坐标分别为A(xA,yA,zA),B(xB,yB,zB),C(xC,yC,zC);三角面片ΔABC在二维坐标系O-XY中的投影三角形ΔA′B′C′各点的坐标分别为A′(xA,yA),B′(xB,yB),C′(xC,yC);
(3-2)利用公式sΔA′B′C′=sΔMB′C′+sΔMA′C′+sΔMA′B′判断动点M是否在ΔA′B′C′上,式中,sΔA′B′C′、sΔMB′C′、sΔMA′C、sΔMA′B′分别表示ΔA′B′C′、ΔMB′C′、ΔMA′C′、ΔMA′B′的面积;根据判断结果执行步骤(3-3)或(3-4);
(3-3)如果公式sΔA′B′C′=sΔMB′C′+sΔMA′C′+sΔMA′B′左右两边相等,则动点M在投影三角形ΔA′B′C′上;
(3-4)如果公式sΔA′B′C′=sΔMB′C′+sΔMA′C′+sΔMA′B′左右两边不相等,则动点M不在投影三角形ΔA′B′C′上;重复步骤(3-1)和(3-2),直至将组成待加工曲面的所有三角面片ΔABC数据读取完成。
3.有益效果
采用本发明提供的技术方案,与已有的公知技术相比,具有如下显著效果:
本发明的一种基于STL三维模型的曲面加工方法,为小曲率曲面的加工提供了一种更加直观简洁的刀位轨迹计算方法,通过将组成待加工曲面的三角面片在三维空间内的计算转化为二维平面内的三角形计算,大大简化了曲面加工刀位轨迹的计算,更加容易实现软件控制,且程序可读性好,运算量少。
附图说明
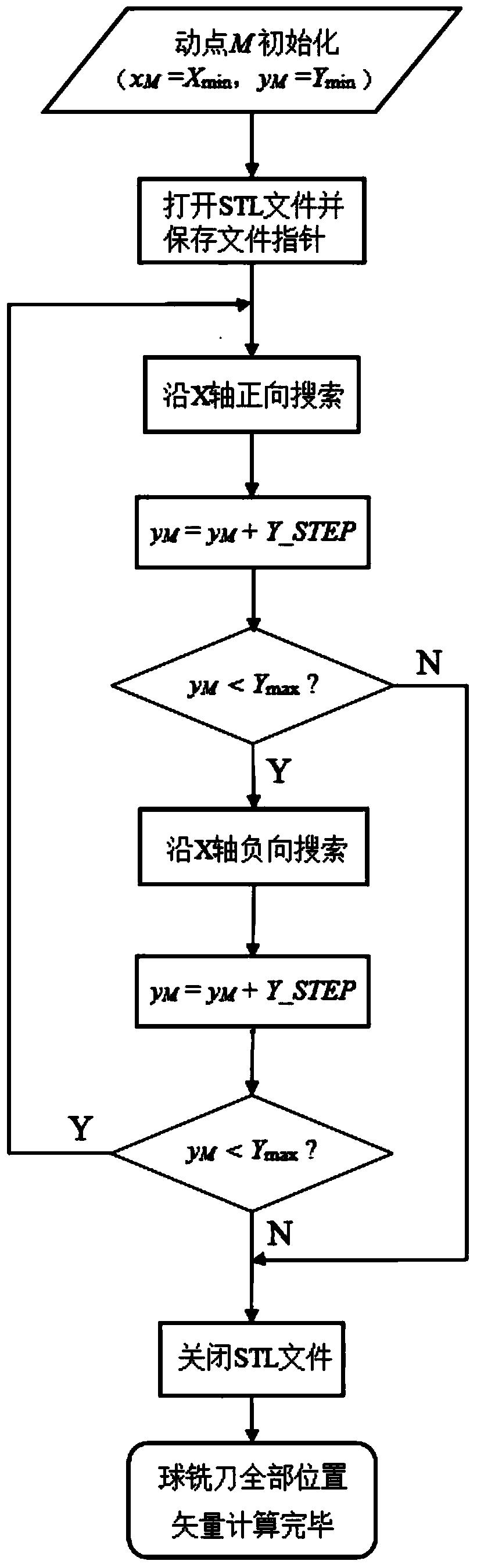
图1为本发明的一种基于STL三维模型的曲面加工方法的球铣刀位置矢量计算流程图;
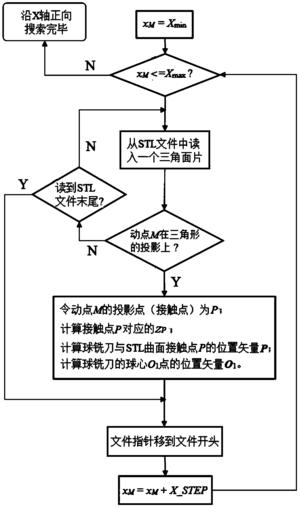
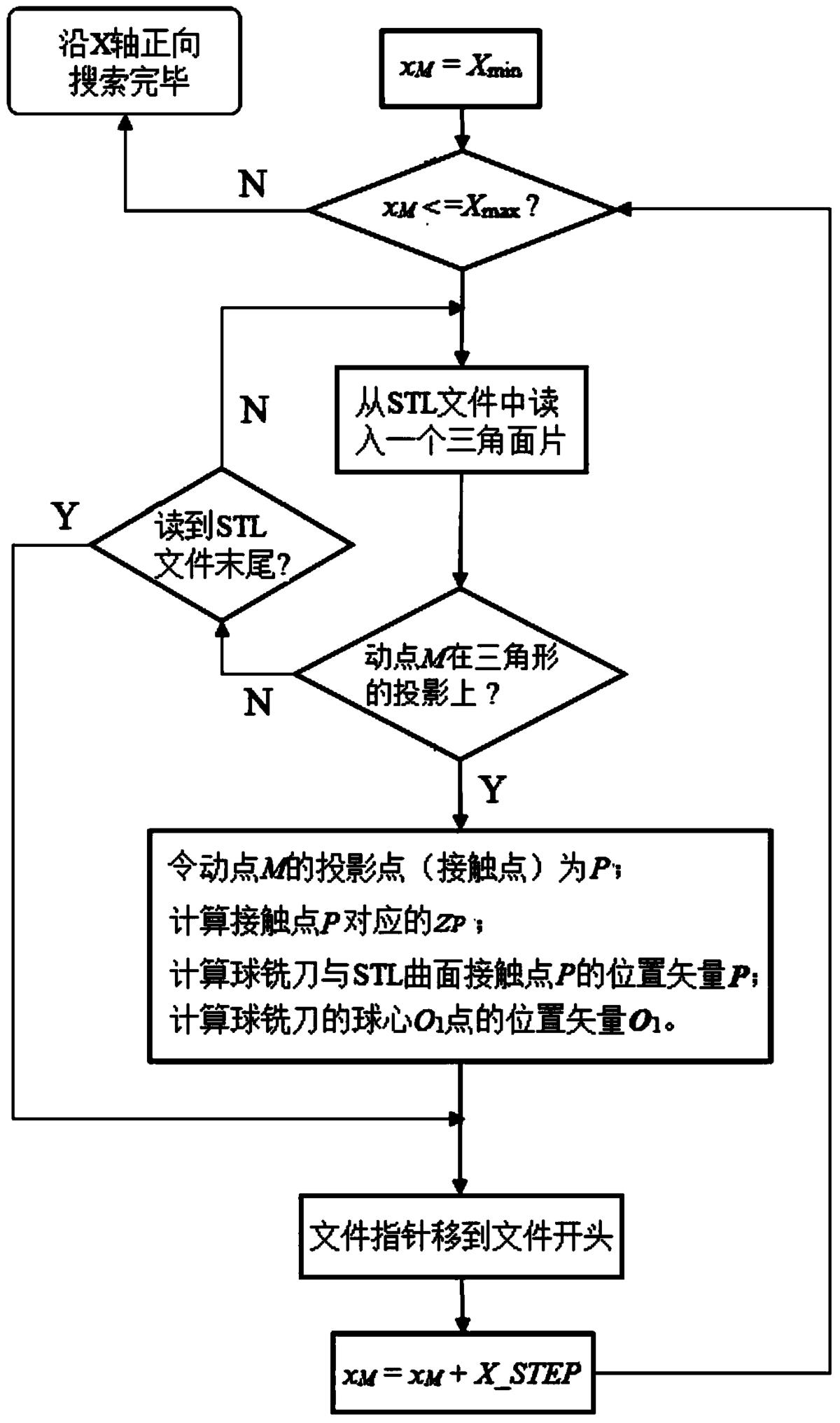
图2为本发明中沿X轴正方向创建动点M的流程图;
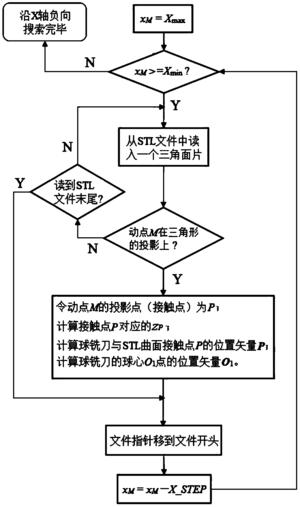
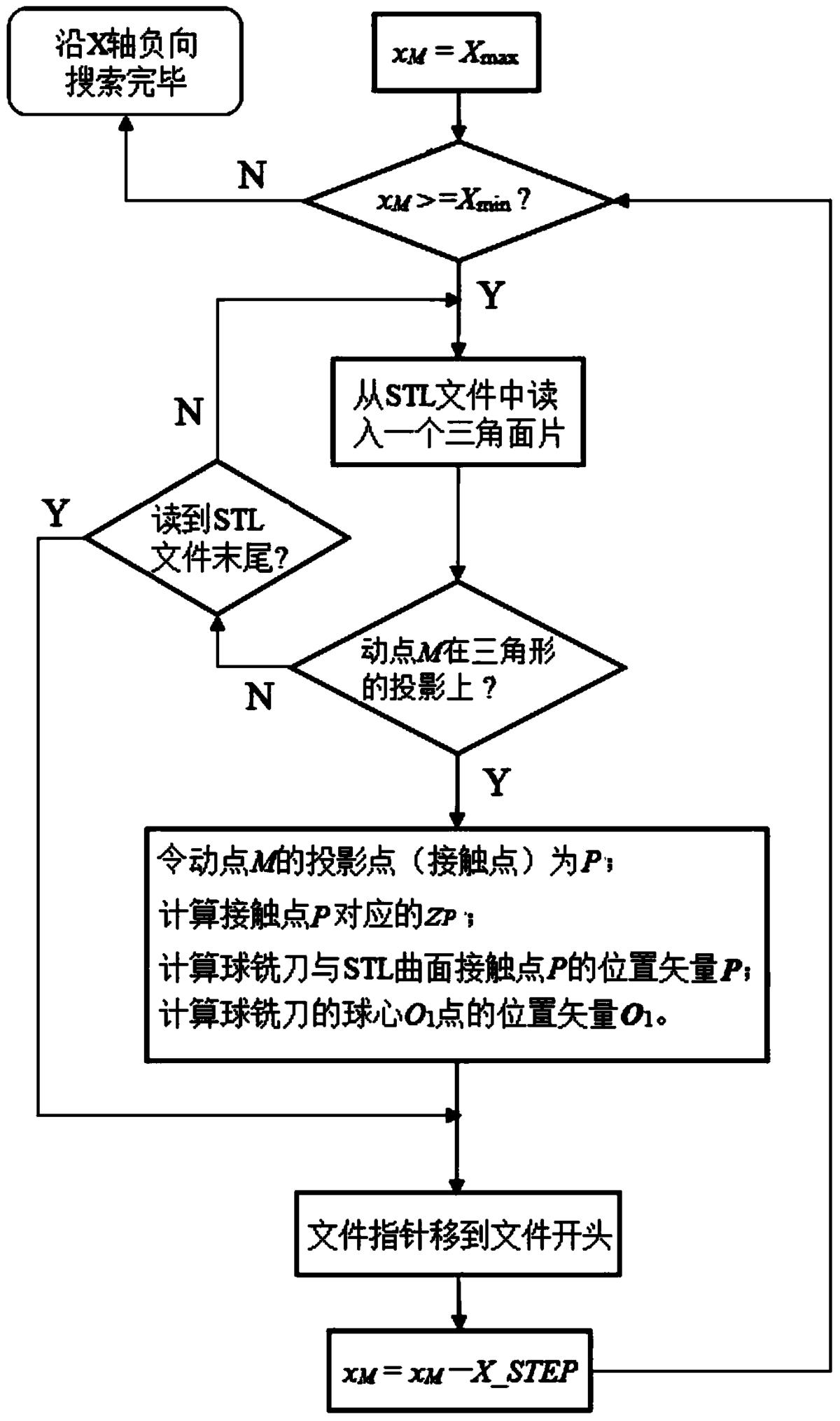
图3为本发明中沿X轴负方向创建动点M的流程图;
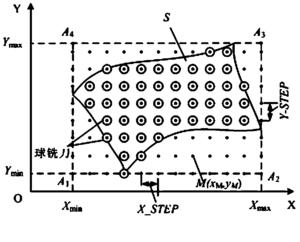
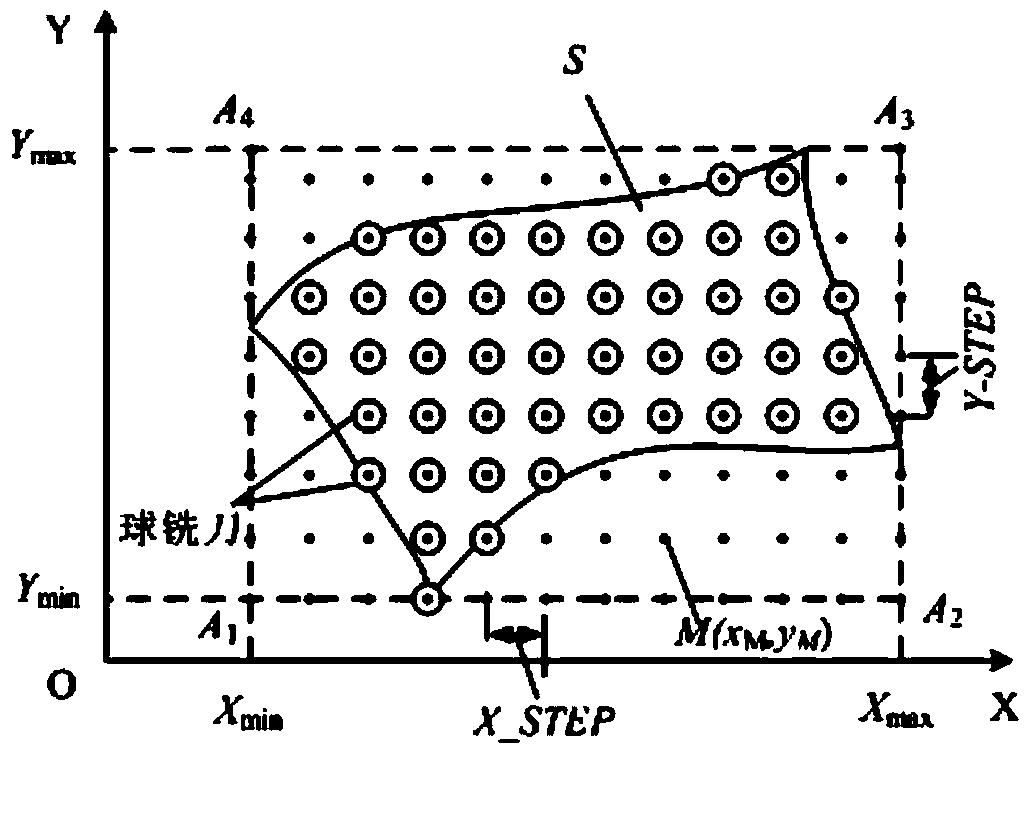
图4为本发明中动点M的创建过程示意图;
图5为本发明中选取三角面片ΔABC中任意一点P的示意图;
图6(a)和图6(b)分别为本发明中选取三角面片ΔABC中任意一点P的不同动态位置示意图;
图7为本发明中球铣刀与STL曲面在P点接触时球心O1的位置矢量计算示意图。
具体实施方式
为进一步了解本发明的内容,结合附图对本发明的刀位轨迹计算原理作详细描述。
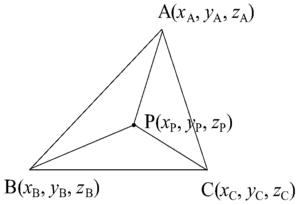
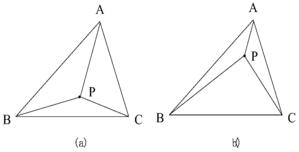
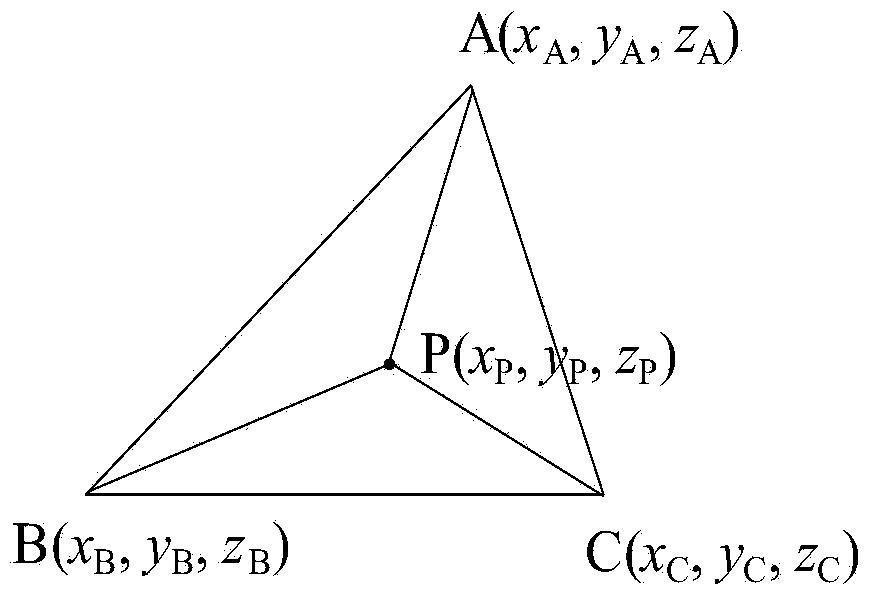
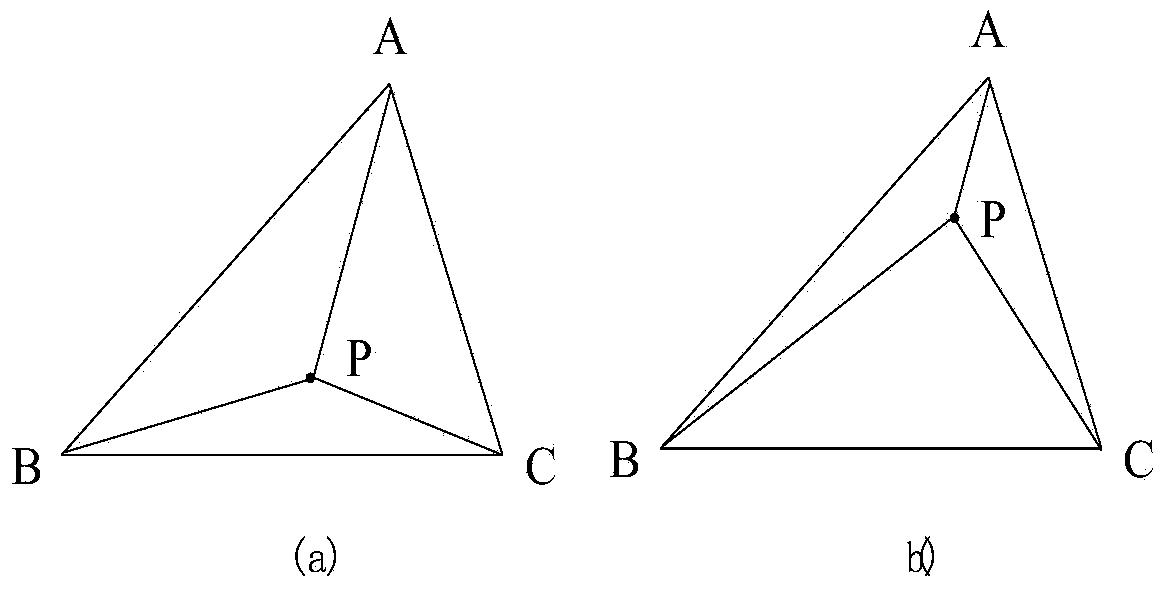
STL文件由多个三角形面片数据的组成,每个三角形面片包括三角形各个顶点的三维坐标及三角形面片的法矢量。如图5所示,已知三维空间三角面片ΔABC在O-XYZ坐标系中各点坐标为A(xA,yA,zA),B(xB,yB,zB),C(xC,yC,zC),ΔABC内部任意一点P在O-XY坐标系中坐标为(xP,yP),现求点P在O-XYZ坐标系中的z轴方向坐标zP。毫无疑问,zP值与zA、zB、zC的值有关。比较图6(a)和图6(b)中的点P与点A的距离,可看出,当点P靠近点A过程中,与点A正对着的三角形ΔPBC的面积(SΔPBC)变大;当点P趋近A点过程中,点P的zP越接近点A的zA,或者说点A的zA对点P的zP影响权重越大,即,zA对zP的影响权重与SΔPBC正比例变化。考察图6(a)和图6(b)中的点P与点B、点C的距离,当点P向点A靠近过程中,点P离点B、点C越来越远,那么zB和zC对zP影响权重越来越小;同时可以发现:点C正对着的三角形ΔPAB的面积(SΔPAB)、点B正对着的三角形ΔPAC的面积(SΔPAC)也越来越小,即,zB对zP的影响权重与SΔPAC正比例变化,zC对zP的影响权重与SΔPAB正比例变化。
上述分析表明,zP值与zA、zB、zC的值正比例相关,且各点对zP的影响权重与各点正对着的三角形的面积SΔPBC、SΔPAC、SΔPAB正比例相关。基于上述分析,提出一种新的用于计算三维空间三角面片内任一点P点的zP值公式为:
z P = z A × s ΔPBC + z B × s ΔPAC + z C × s ΔPAB s ΔABC = z A s ΔPBC s ΔABC + z B s ΔPAC s ΔABC + z C s ΔPAB s ΔABC - - - ( 1 ) ]]>
z P = z A s ΔPBC s ΔABC + z B s ΔPAC s ΔABC + z C s ΔPAB s ΔABC - - - ( 2 ) ]]>
式中:SΔPBC、SΔPAC、SΔPAB、SΔABC分别表示ΔPBC、ΔPAC、ΔPAB、ΔABC的面积。
上式(2)中,SΔPBC、SΔPAC、SΔPAB未知,因此zP无法求出。假设ΔABC在O-XY坐标系中的投影为ΔA′B′C′,且其各点坐标为A′(xA,yA),B′(xB,yB),C′(xC,yC),点P在O-XY坐标系中的投影为点P′(xP,yP)。因此,点A′、B′、C′、P′在O-XY坐标系中的坐标都为已知,所以可求出上述三角形面积分别为:SΔP’B’C’、SΔP’A’C’、SΔP’A’B’、SΔA’B’C’。因为ΔP′B′C′、ΔP′A′C′、ΔP′A′B′、ΔA′B′C′分别为ΔPBC、ΔPAC、ΔPAB、ΔABC在O-XY坐标系中的投影,因此上述三角形面积之间存在以下关系:
s ΔPBC s ΔABC = s ΔP ′ B ′ C ′ s Δ ′ B ′ C ′ - - - ( 3 ) ]]>
s ΔPAC s ΔABC = s ΔP ′ A ′ C ′ s Δ ′ B ′ C ′ - - - ( 3 ) ]]>
s ΔPAB s ΔABC = s ΔP ′ A ′ B ′ s Δ ′ B ′ C ′ - - - ( 5 ) ]]>
将式(3)、(4)、(5)代入式(2)中的式(6)为:
z P = z A s ΔP ′ B ′ C ′ s ΔA ′ B ′ C ′ + z B s ΔP ′ A ′ C ′ s ΔA ′ B ′ C ′ + z C s ΔP ′ A ′ B ′ s ΔA ′ B ′ C ′ = z A × s ΔP ′ B ′ C ′ + z B × s ΔP ′ A ′ C ′ + z C × s ΔP ′ A ′ B ′ s ΔA ′ B ′ C ′ - - - ( 6 ) ]]>
因此,将需要进行的三维空间内三角面片面积计算问题转化为二维平面内三角形面积计算,简化了计算。而已知二维平面内ΔABC各点坐标为A(xA,yA),B(xB,yB),C(xC,yC),则其面积为:
s ΔABC = | x A y B + x B y C + x C y A - x B y A - x C y B - x A y C 2 | - - - ( 2 ) ]]>
因此,由式(6)和式(7)可计算出三维空间三角面片内任一点的z坐标。并且,式(6)的正确性已经过实际数据验证。
下面结合实施例对本发明作进一步的描述。
实施例
参见图1、图2和图3所示,本实施例的一种基于STL三维模型的曲面加工方法,主要适用于铣削加工小曲率STL格式曲面,STL格式曲面采用ASCII明码格式,并采用Visual C++实现对三角片面数据的读取,其包括以下步骤:
(1)已知待加工曲面的STL三维模型,将曲面的三维模型投影到二维坐标系O-XY中,得到投影面S;组成待加工曲面的若干三角面片ΔABC在二维坐标系O-XY中的投影为三角形ΔA′B′C′;
(2)创建并读取动点M(xM,yM);如图2、图3和图4所示,动点M(xM,yM)的创建过程如下:
(2-1)测出投影面S在二维坐标系O-XY的X轴方向上的最小值Xmin和最大值Xmax,以及Y轴方向上的最小值Ymin和最大值Ymax;由Xmin、Xmax、Ymin和Ymax坐标值构造矩形A1A2A3A4;并设定球铣刀移动的步长(即图4中的X_STEP)和行距(即图4中的Y_STEP);
(2-2)将动点M(xM,yM)初始化,初始位置为矩形A1A2A3A4的左下角顶点A1(Xmin,Ymin),即xM=Xmin,yM=Ymin;
(2-3)将动点M(xM,yM)沿平行X轴正方向逐一移动一个步长X_STEP,并记下每一个点的坐标,直到xM>Xmax,完成平行X轴的一行动点M的创建(如图2所示流程);
(2-4)将动点M(xM,yM)沿平行Y轴正方向移动一个行距Y_STEP,令xM=Xmax,并沿平行X轴负方向逐一移动一个步长X_STEP,直到xMmin,完成平行X轴的下一行动点M的创建(如图3所示流程);将动点M(xM,yM)沿平行Y轴正方向移动一个行距Y_STEP;
(2-5)令xM=Xmin,重复步骤(2-3)、(2-4),直到yM>Ymax,完成整个矩形A1A2A3A4区域内的动点M的创建;
(3)判断动点M(xM,yM)是否在投影面S中的某个投影三角形ΔA′B′C′上,包括以下三种情况:a、动点M在三角形内部;b、动点M在三角形某个边上;c、动点M在三角形某个顶点上;判断的具体方法为:
(3-1)读取一个三角面片ΔABC,ΔABC各点的坐标分别为A(xA,yA,zA),B(xB,yB,zB),C(xC,yC,zC);三角面片ΔABC在二维坐标系O-XY中的投影三角形ΔA′B′C′各点的坐标分别为A′(xA,yA),B′(xB,yB),C′(xC,yC);
(3-2)利用公式sΔA′B′C′=sΔMB′C′+sΔMA′C′+sΔMA′B′判断动点M是否在ΔA′B′C′上,式中,sΔA′B′C′、sΔMB′C′、sΔMA′C、sΔMA′B′分别表示ΔA′B′C′、ΔMB′C′、ΔMA′C′、ΔMA′B′的面积;根据判断结果执行步骤(3-3)或(3-4);
(3-3)如果公式sΔA′B′C′=sΔMB′C′+sΔMA′C′+sΔMA′B′左右两边相等,则动点M在投影三角形ΔA′B′C′上;执行步骤(4);
(3-4)如果公式sΔA′B′C′=sΔMB′C′+sΔMA′C′+sΔMA′B′左右两边不相等,则动点M不在投影三角形ΔA′B′C′上;重复步骤(3-1)和(3-2),直至将组成待加工曲面的所有三角面片ΔABC数据读取完成;执行步骤(5);
(4)如果动点M在投影面S中的某个投影三角形ΔA′B′C′上,求出动点M(xM,yM)对应的投影点P在三维坐标系O-XYZ中的坐标(xP,yP,zP),即球铣刀与对应三角面片ΔABC的接触点坐标,其中:xP=xM,yP=yM,
z p = z A × S Δ MB ′ C ′ + z B × S Δ MA ′ C ′ + z C × S Δ MA ′ B ′ S Δ A ′ B ′ C ′ , ]]>
式中:zA、zB和zC分别表示三角面片ΔABC中的A、B和C三点的在O-XYZ坐标系中的z轴坐标,SΔMB′C′、SΔMA′C′、SΔMA′B′和SΔA′B′C′分别表示ΔMB′C′、ΔMA′C′、ΔMA′B′和ΔA′B′C′的面积;则球铣刀与曲面的接触点P(xP,yP,zP)在O-XYZ坐标系中的位置矢量为:
P=(xp,yp,zp)T;
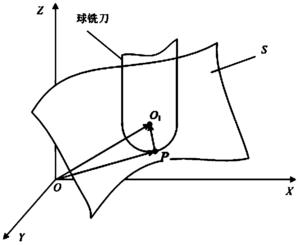
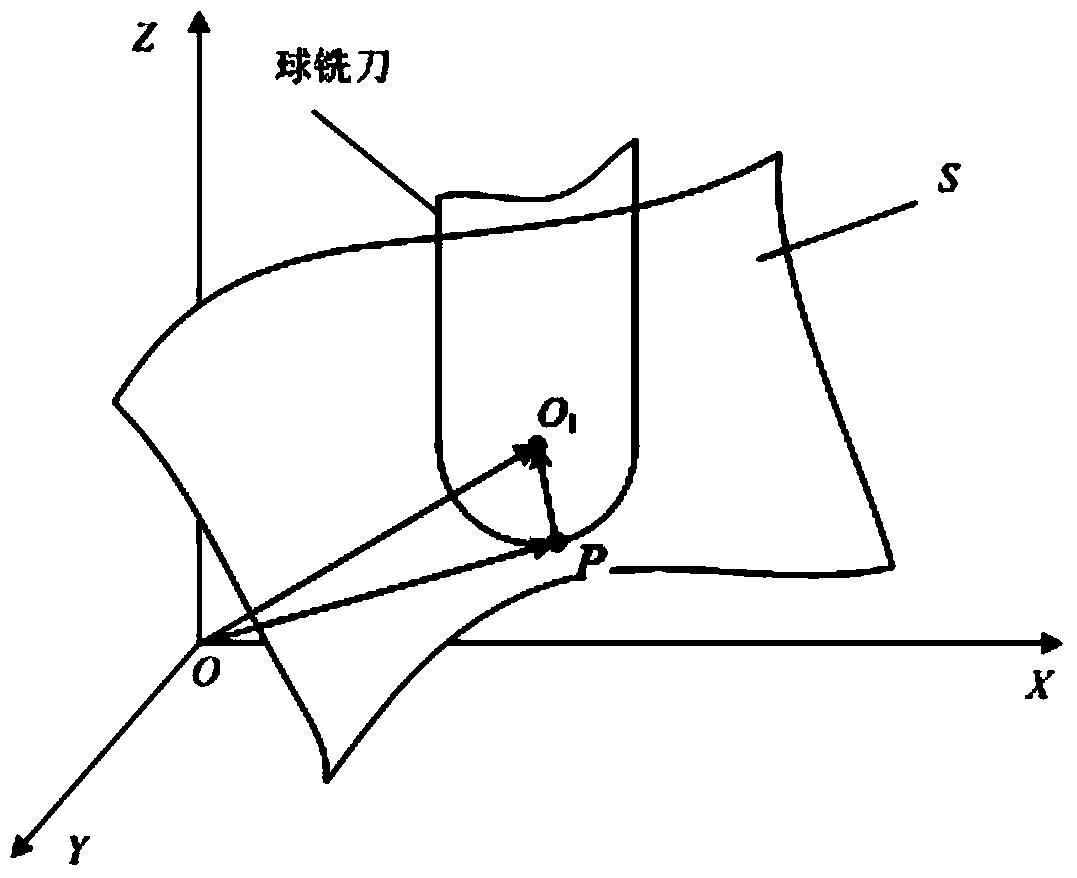
进而,如图7所示,求出球铣刀的球心O1点在O-XYZ坐标系中的位置矢量O1为:
O 1 = P + PO 1 = P + r PO 1 | PO 1 | , ]]>
式中:r为球铣刀的半径,为矢量PO1的单位矢量;因STL文件中给出了三角面片的法矢量形式为“facet normal x y z”,因此,等于球铣刀与曲面接触点P所在三角面片ΔABC的法矢量的单位矢量;
PO 1 | PO 1 | = ( x x 2 + y 2 + z 2 , y x 2 + y 2 + z 2 , z x 2 + y 2 + z 2 ) T , ]]>
因此,
O 1 = P + PO 1 = P + r ( x x 2 + y 2 + z 2 , y x 2 + y 2 + z 2 , z x 2 + y 2 + z 2 ) T , ]]>
式中:即为球铣刀与曲面接触点P所在三角面片ΔABC的法矢量的单位矢量;求出球铣刀的球心O1在O-XYZ坐标系中的位置矢量O1后,重复步骤(2),读取下一个动点M(xM,yM),并重复步骤(3),直至将所有动点M读取完毕;
(5)如果动点M不在投影面S中的某个投影三角形ΔA′B′C′上,则重复步骤(2),读取下一个动点M(xM,yM),并重复步骤(3),直至将所有动点M读取完毕;
(6)顺序连接各点即可得到球铣刀加工STL曲面的刀位轨迹;该刀位轨迹是由许多微小直线段组成,即用微小直线段来逼近STL曲面,可以通过减小刀具移动时步长(X_STEP)和行距(Y_STEP)来减小微小直线段逼近STL曲面时产生的逼近误差。
本发明的一种基于STL三维模型的曲面加工方法,其刀位轨迹的计算方法适用于各点法矢量与Z轴夹角不大的STL曲面。在构造矩形A1A2A3A4内实现球铣刀的位置搜索和计算,减少了数据采集量,通过将组成待加工曲面的三角面片在三维空间内的计算转化为二维平面内的三角形计算,大大简化了曲面加工刀位轨迹的计算,更加容易实现软件控制,且程序可读性好,运算量少。
以上示意性地对本发明及其实施方式进行了描述,该描述没有限制性,附图中所示的也只是本发明的实施方式之一,实际的结构并不局限于此。所以,如果本领域的普通技术人员受其启示,在不脱离本发明创造宗旨的情况下,不经创造性地设计出与该技术方案相似的结构方式及实施例,均应属于本发明的保护范围。
 价值度评估
价值度评估
技术价值
经济价值
法律价值
0 0 062.0分
0 50 75 100专利价值度是通过科学的评估模
型对专利价值进行量化的结果,
基于专利大数据针对专利总体特
征指标利用计算机自动化技术对
待评估专利进行高效、智能化的
分析,从技术、经济和法律价值
三个层面构建专利价值评估体
系,可以有效提升专利价值评估
的质量和效率。
总评:62.0分
该专利价值中等 (仅供参考)
本专利文献中包含【1 个实施例】、【1 个技术分类】,从一定程度上而言上述指标的数值越大可以反映出所述专利的技术保护及应用范围越广。 【专利权的维持时间11 年】专利权的维持时间越长,其价值对于权利人而言越高。 尤其重要是,该专利 【权利转移1 次】、 都从侧面反应出该专利的技术、经济和法律价值。
技术价值 31.0
该指标主要从专利申请的著录信息、法律事件等内容中挖掘其技术价值,专利类型、独立权利要求数量、无效请求次数等内容均可反映出专利的技术性价值。 技术创新是专利申请的核心,若您需要进行技术借鉴或寻找可合作的项目,推荐您重点关注该指标。
部分指标包括:
授权周期(发明)
29 个月独立权利要求数量
1 个从属权利要求数量
2 个说明书页数
6 页实施例个数
1 个发明人数量
6 个被引用次数
0 次引用文献数量
0 个优先权个数
0 个技术分类数量
1 个无效请求次数
0 个分案子案个数
0 个同族专利数
0 个专利获奖情况
无保密专利的解密
否经济价值 9.0
该指标主要指示了专利技术在商品化、产业化及市场化过程中可能带来的预期利益。 专利技术只有转化成生产力才能体现其经济价值,专利技术的许可、转让、质押次数等指标均是其经济价值的表征。 因此,若您希望找到行业内的运用广泛的热点专利技术及侵权诉讼中的涉案专利,推荐您重点关注该指标。
部分指标包括:
申请人数量
1申请人类型
院校许可备案
0 次权利质押
0 次权利转移
1 个海关备案
否法律价值 22.0
该指标主要从专利权的稳定性角度评议其价值。专利权是一种垄断权,但其在法律保护的期间和范围内才有效。 专利权的存续时间、当前的法律状态可反映出其法律价值。故而,若您准备找寻权属稳定且专利权人非常重视的专利技术,推荐您关注该指标。
部分指标包括:
存活期/维持时间
11法律状态
有权-审定授权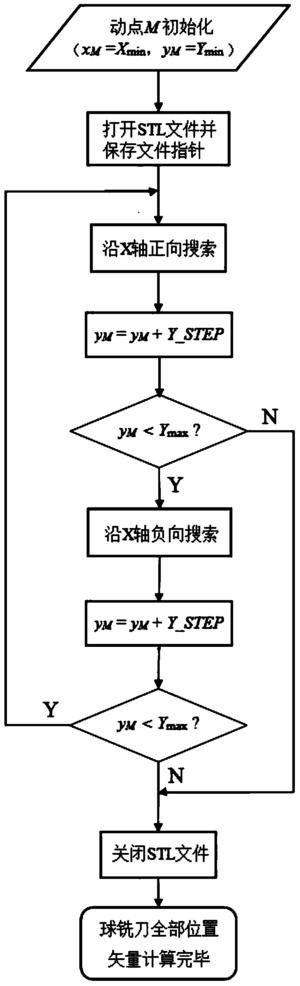

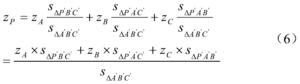

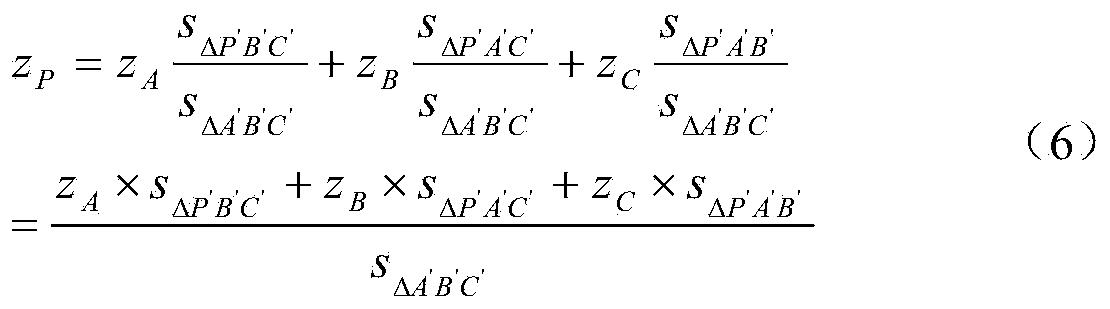








 苏公网安备 32041202001399号
苏公网安备 32041202001399号



 loading...
loading...